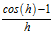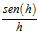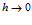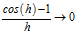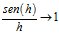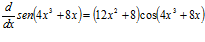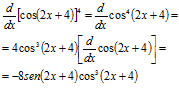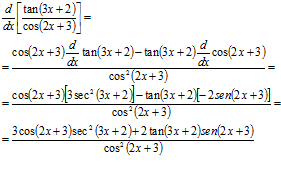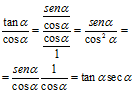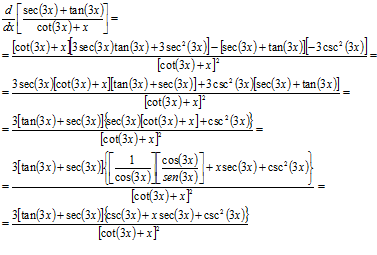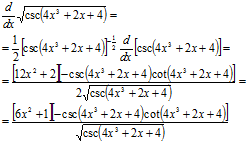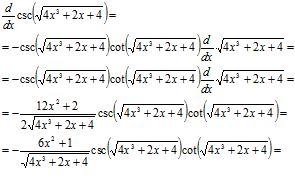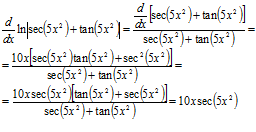¡Haz clic para puntuar!

(Votos: 10 Promedio: 4.7)

Derivadas de funciones trigonometricas.

Recordemos que la derivada se define como

102017 1657 Derivadastr1 .

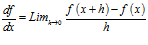Sea la función trigonométrica 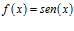102017 1657 Derivadastr2 , su derivada está dada por

102017 1657 Derivadastr3

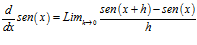
Las identidades trigonométricas establecen que

102017 1657 Derivadastr4

por lo tanto,

102017 1657 Derivadastr5

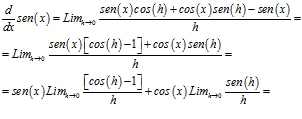
Para poder resolver estos límites, analizaremos el resultado para valores pequeños de h

Así que

102017 1657 Derivadastr11

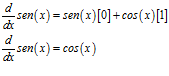
Sea la función trigonométrica 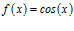102017 1657 Derivadastr12 , su derivada está dada por

102017 1657 Derivadastr13

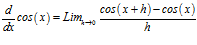
que utilizando identidades trigonométricas se puede expresar como

102017 1657 Derivadastr14

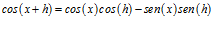
y, por lo tanto,

102017 1657 Derivadastr15

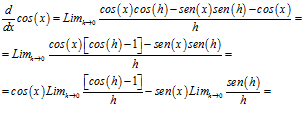
y dada la tabla anterior

102017 1657 Derivadastr16

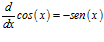
Al utilizar la regla de la cadena, se pueden generalizar estas fórmulas a

102017 1657 Derivadastr17

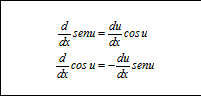
A partir de estas dos derivadas se pueden obtener las de las demás funciones trigonométricas.

102017 1657 Derivadastr18

102017 1657 Derivadastr19

102017 1657 Derivadastr20

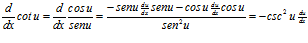
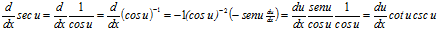
De esta manera se establece que:

102017 1657 Derivadastr21

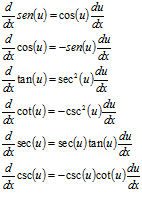
Algunos ejercicios:

	Es importante recalcar que el argumento de la función no se alteró al realizar la derivada. Solo se puede cambiar el argumento de una función trigonométrica usando identidades trigonométricas.
	En este ejercicio se resaltan varios puntos: El exponente que aparece al lado de la función trigonométrica indica una operación sobre el resultado de la función trigonométrica: primero se obtiene el resultado de la función trigonométrica y posteriormente se eleva al exponente dado. Es importante destacar que si el exponente es -1 puede confundirse con las funciones inversas. Una función trigonométrica inversa no es la función con exponente -1. El -1 que aparece en la función inversa solo es una notación y no un exponente. En el segundo renglón de la derivada se está resolviendo utilizando la regla de la cadena. En el último renglón ya está resuelta tanto la derivada del argumento de la función trigonométrica como el producto con la constante.
	El argumento de la funciones trigonométricas es distinto, por lo tanto, no se puede hacer: Sin embargo, tener este tipo de identidades y operaciones a la mano resulta muy útil puesto que puede simplificar muchas operaciones. La última expresión se puede simplificar utilizando identidades trigonométricas.

Las últimas dos derivadas sirven para reafirmar la diferencia entre una raíz cuadrada aplicada a la función trigonométrica y al argumento de la misma.