Visite nuestra página integrales.es
DERIVADAS FUNCIONES
HIPERBÓLICAS INVERSAS
156 EJERCICIOS RESUELTOS
Versión 1-5-2014
|
FORMULAS BÁSICAS DE DERIVACIÓN |
||
|
FORMAS SIMPLES |
Nº |
FORMAS COMPUESTAS |
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
31 |
|
|
|
REGLAS BÁSICAS DE DERIVACIÓN |
|
1ª) LA DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN es igual a la constante por la derivada de la función: |
|
2ªa) LA DERIVADA DE UNA SUMA DE FUNCIONES es igual a la suma de las derivadas de las funciones: |
|
2ªb) LA DERIVADA DE UNA DIFERENCIA DE FUNCIONES es igual a la diferencia de las derivadas de las funciones: |
|
3ª) LA DERIVADA DE UN PRODUCTO DE FUNCIONES es igual a la derivada de la primera función por la segunda función sin derivar más la primera función sin derivar por la derivada de la segunda función: |
|
4ª) LA DERIVADA DE UN COCIENTE DE FUNCIONES es igual a la derivada de la función del numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la derivada de la función del denominador, dividido todo ello por la función del denominador al cuadrado: |
|
5ª) LA DERIVADA DE UNA FUNCIÓN ELEVADA A OTRA es igual a la derivada de la expresión como exponencial más la derivada de la expresión como potencial: |
DERIVADA DE LA FUNCIÓN
ARGUMENTO SENO HIPÉRBOLICO
|
FÓRMULA 25 simple
LA DERIVADA DEL ARGUMENTO SENO HIPERBÓLICO DE x es igual al logaritmo neperiano de x más la raíz cuadrada de la unidad más x al cuadrado |
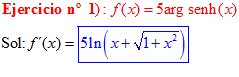
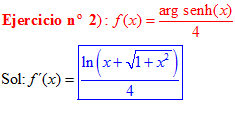
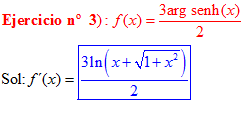
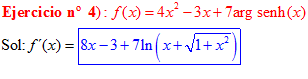
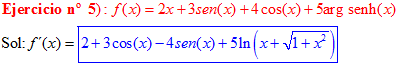
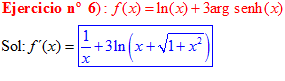
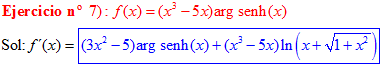
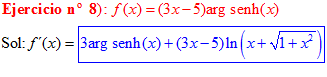

|
FÓRMULA 25 compuesta
LA DERIVADA DEL ARGUMENTO SENO HIPERBÓLICO DE una función de x es igual a la derivada de la función por el logaritmo neperiano de la función de x más la raíz cuadrada de la unidad más la función al cuadrado |
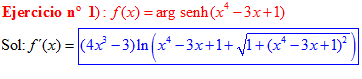
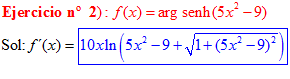
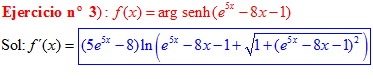
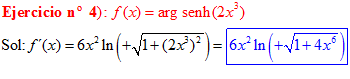
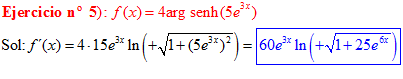
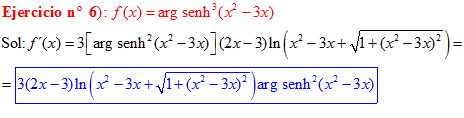


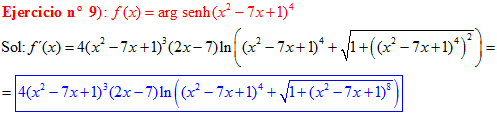
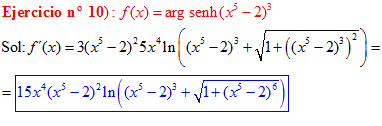
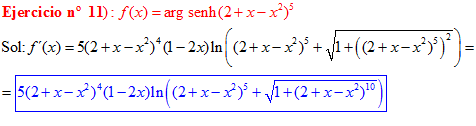
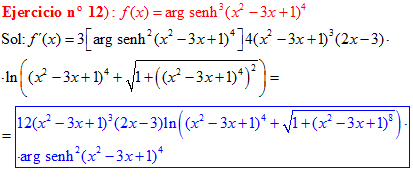
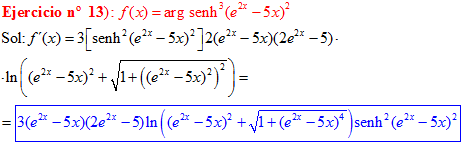
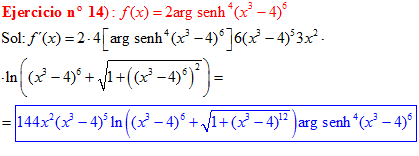
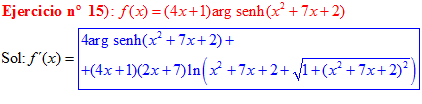
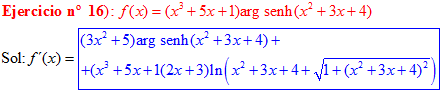
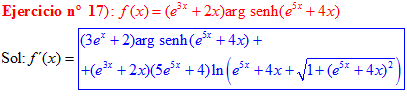
❊❊❊❊❊ FIN FÓRMULA 25 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO COSENO HIPÉRBOLICO
|
FÓRMULA 26 simple
LA DERIVADA DEL ARGUMENTO COSENO HIPERBÓLICO DE x es igual al logaritmo neperiano de x más la raíz cuadrada de x al cuadrado menos la unidad |
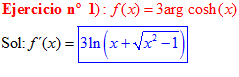
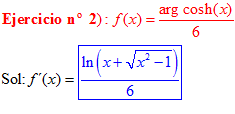
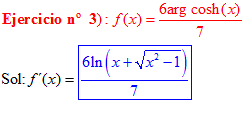
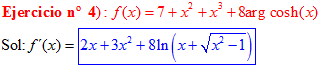
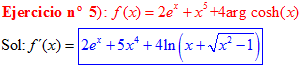
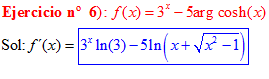
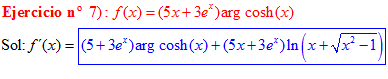

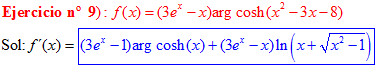
|
FÓRMULA 26 compuesta
LA DERIVADA DEL ARGUMENTO COSENO HIPERBÓLICO DE una función de x es igual a la derivada de la función por el logaritmo neperiano de la función de x más la raíz cuadrada de la función al cuadrado menos la unidad |
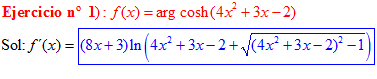
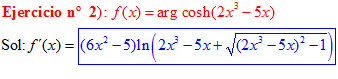
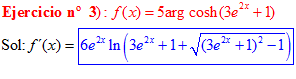

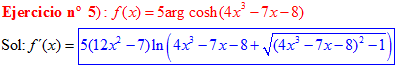

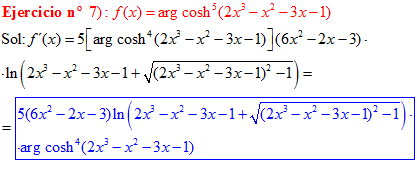
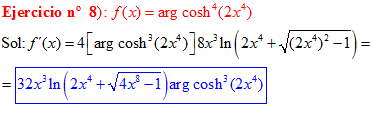
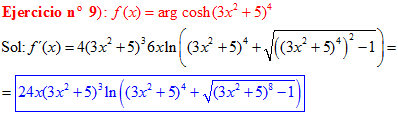
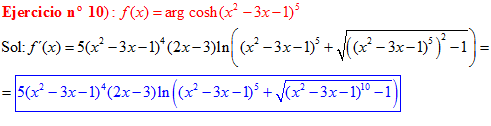
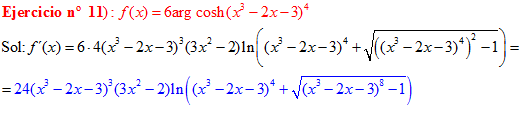
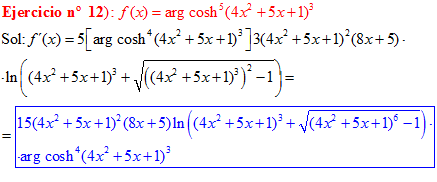
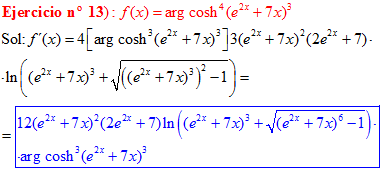
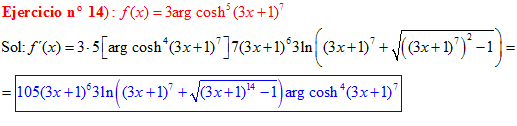
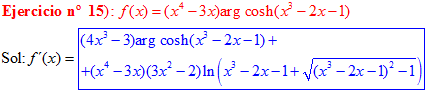
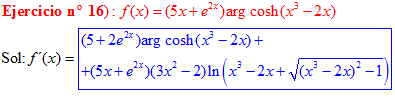
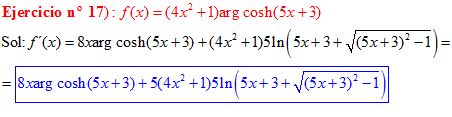
❊❊❊❊❊ FIN FÓRMULA 26 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO TANGENTE HIPÉRBOLICA
|
FÓRMULA 27 simple
LA DERIVADA DEL ARGUMENTO TANGENTE HIPERBÓLICA DE x es igual a un medio del logaritmo neperiano de uno más x dividido entre uno menos la variable x |
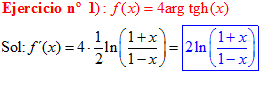
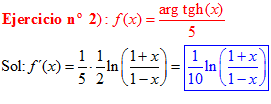
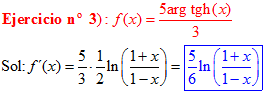
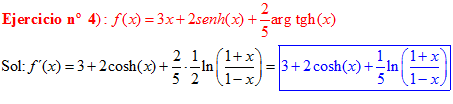
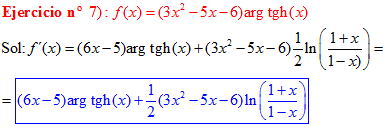
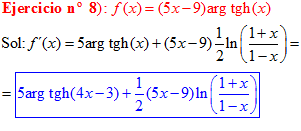
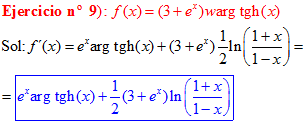
|
FÓRMULA 27 compuesta
LA DERIVADA DEL ARGUMENTO TANGENTE HIPERBÓLICA DE una función de x es igual a la derivada de la función por un medio del logaritmo neperiano de uno más la función dividido entre uno menos la función de x |
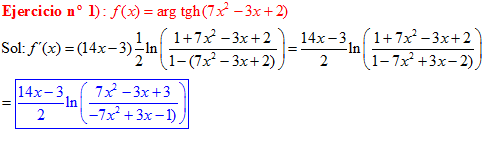
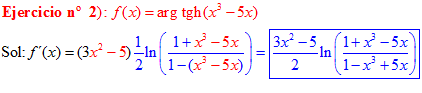
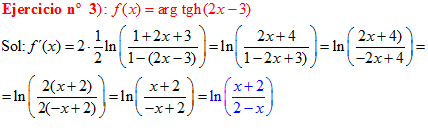
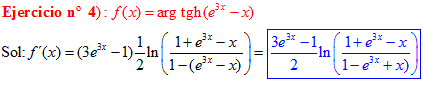
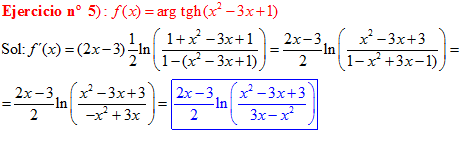
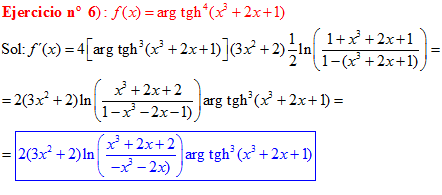
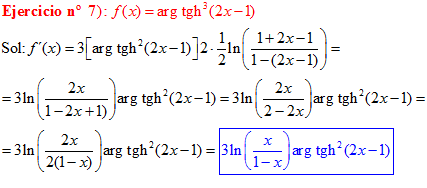
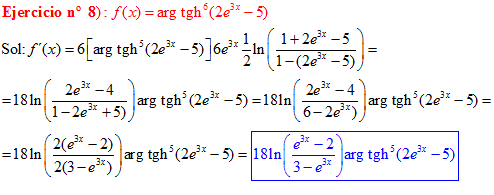
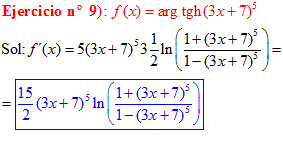
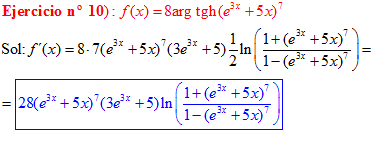
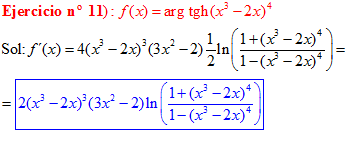
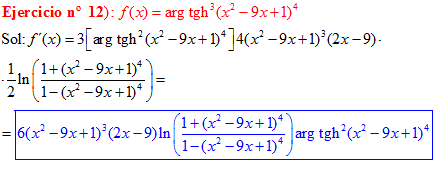
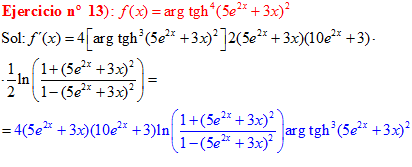
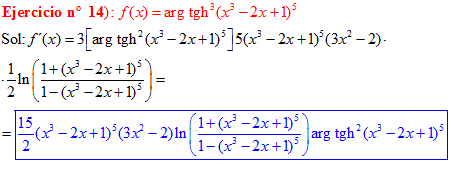
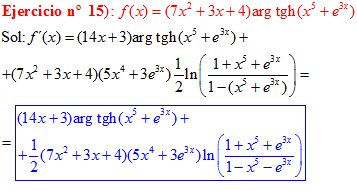
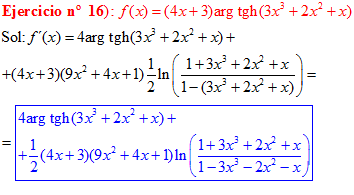
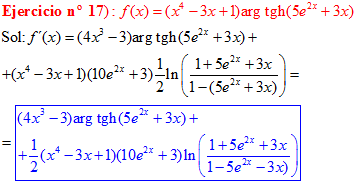
❊❊❊❊❊ FIN FÓRMULA 27 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO COTANGENTE
HIPÉRBOLICA
|
FÓRMULA 28 simple
LA DERIVADA DEL ARGUMENTO COTANGENTE HIPERBÓLICA DE x es igual a un medio del logaritmo neperiano de x más uno dividido entre x menos uno |
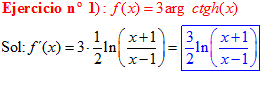
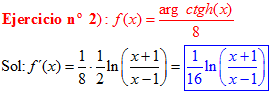
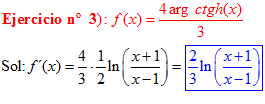
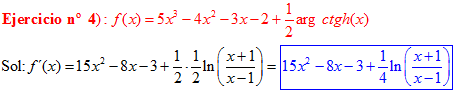
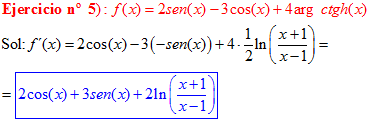
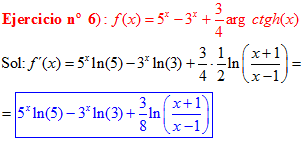
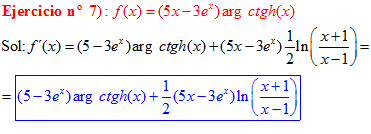
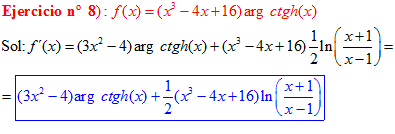
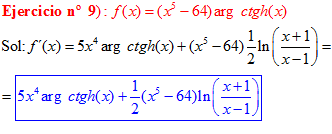
|
FÓRMULA 28 compuesta
LA DERIVADA DEL ARGUMENTO COTANGENTE HIPERBÓLICA DE una función de x es igual a la derivada de la función por un medio del logaritmo neperiano de la función más uno dividido entre la función menos uno |
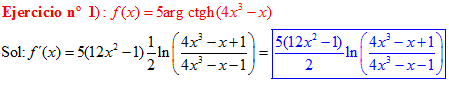
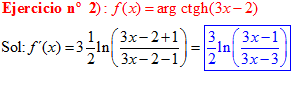
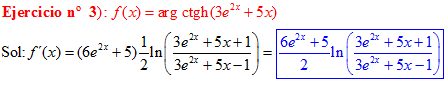
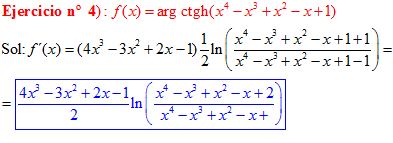

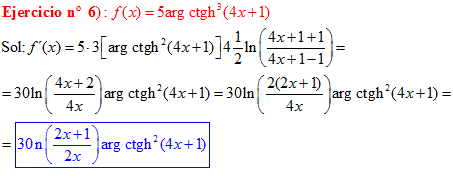
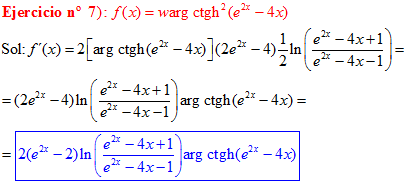
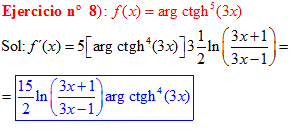
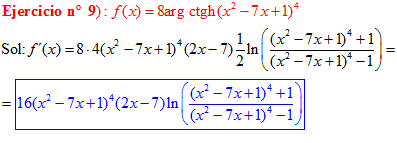
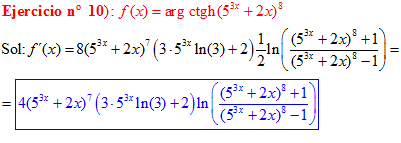
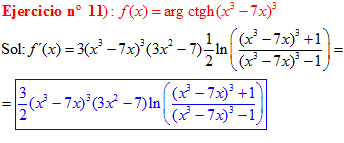
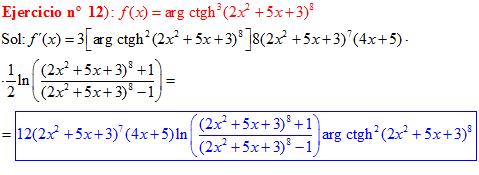
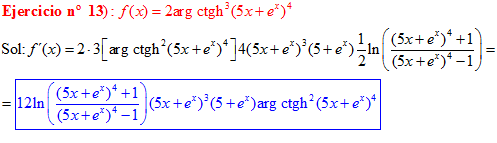
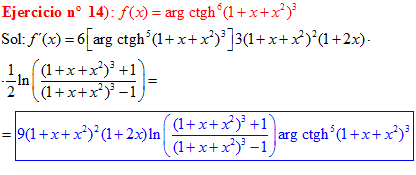
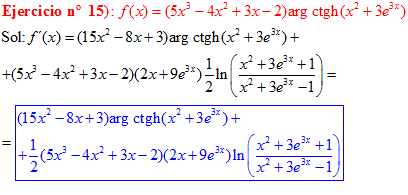
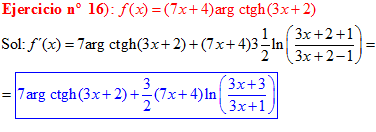
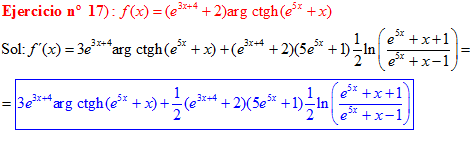
❊❊❊❊❊ FIN FÓRMULA 28 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO SECANTE HIPÉRBOLICA
|
FÓRMULA 29 simple
LA DERIVADA DEL ARGUMENTO SECANTE HIPERBÓLICA DE x es igual al logaritmo neperiano del cociente de uno más la raíz cuadrada de uno menos x al cuadrado dividido entre x |
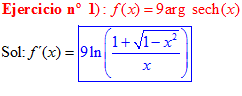
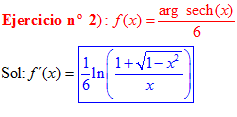
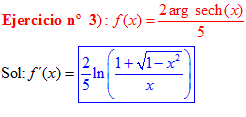
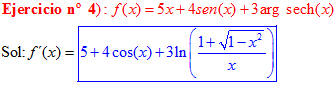
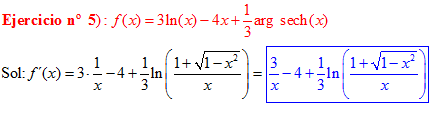
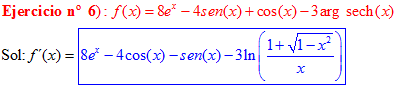

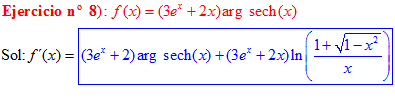
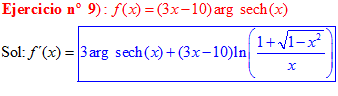
|
FÓRMULA 29 compuesta
LA DERIVADA DEL ARGUMENTO SECANTE HIPERBÓLICA DE una función de x es igual a la derivada de la función por el logaritmo neperiano del cociente de uno más la raíz cuadrada de uno menos la función al cuadrado dividido entre la función |
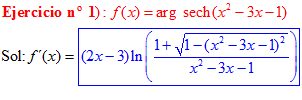
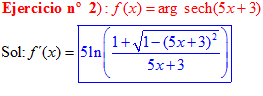
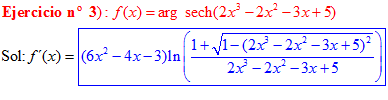
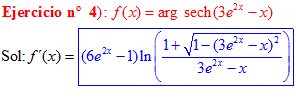
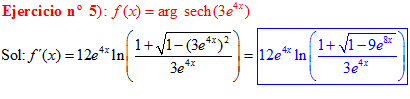



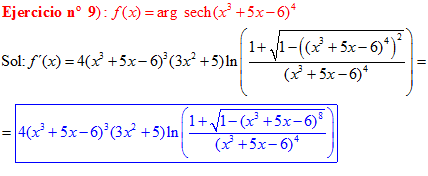
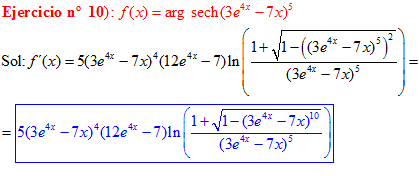
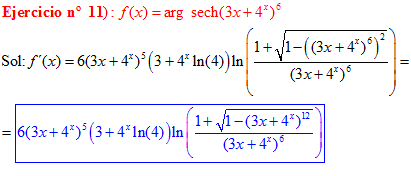
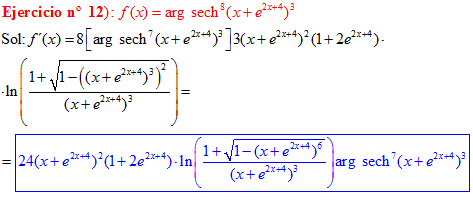
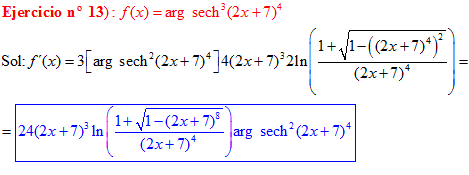
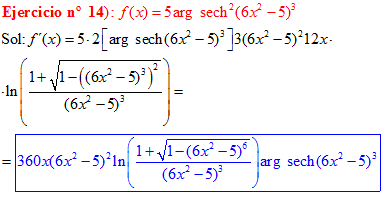
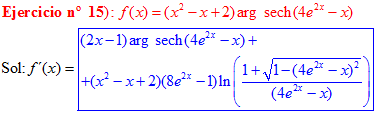

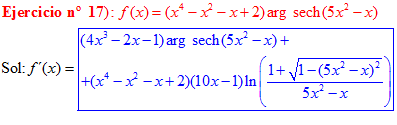
❊❊❊❊❊ FIN FÓRMULA 29 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO COSECANTE
HIPÉRBOLICA
|
FÓRMULA 30 simple
LA DERIVADA D DEL ARGUMENTO COSECANTE HIPERBÓLICA DE x es igual al logaritmo neperiano de la expresión uno partido por x más la raíz cuadrada de uno más x al cuadrado partido por valor absoluto de x |
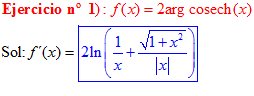
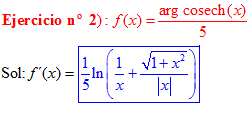
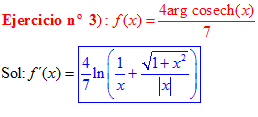

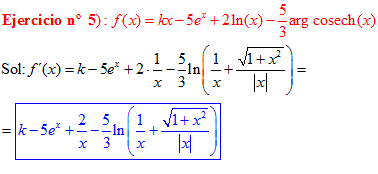
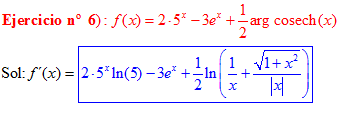
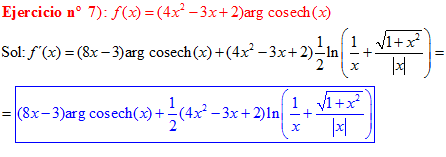
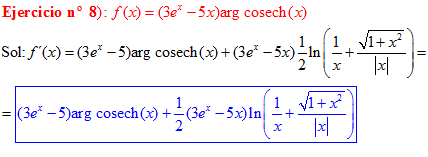
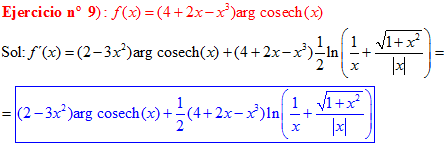
|
FÓRMULA 30 compuesta
LA DERIVADA DEL ARGUMENTO COSECANTE HIPERBÓLICA DE una función de x es igual a la derivada de la función por el logaritmo neperiano de la expresión uno partido por la función más la raíz cuadrada de uno más la función al cuadrado partido por valor absoluto de la función |

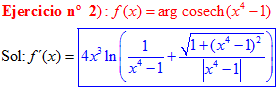
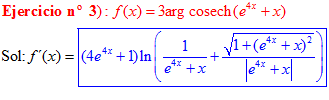
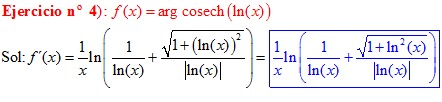
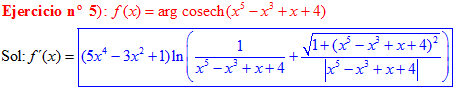

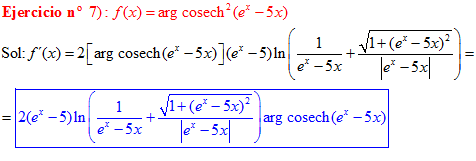
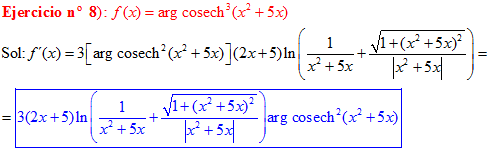
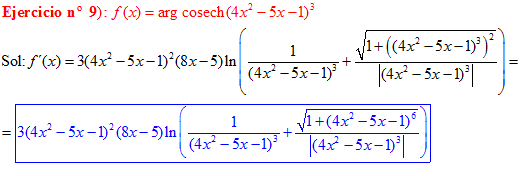
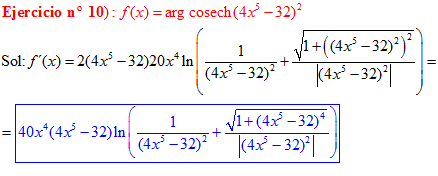
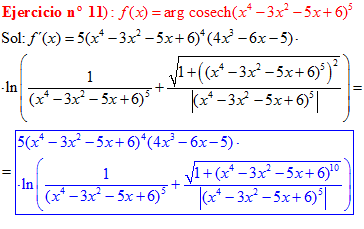
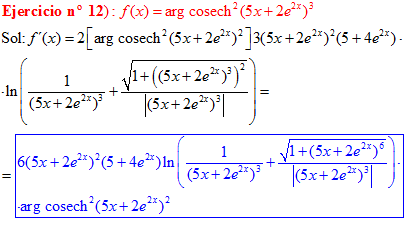
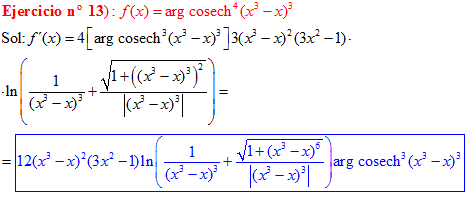
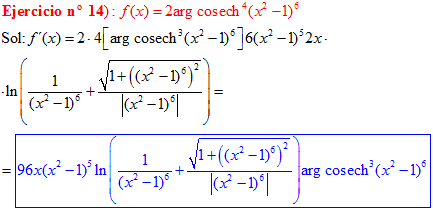
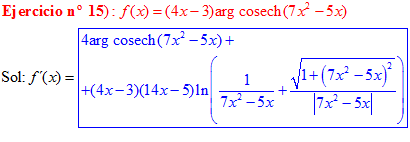
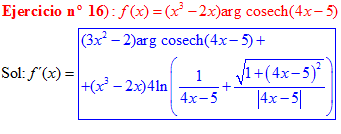
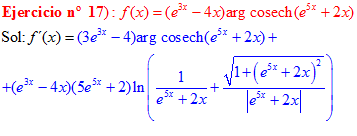
❊❊❊❊❊ FIN FÓRMULA 30 ❊❊❊❊❊


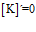
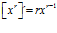
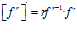
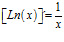
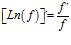
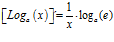
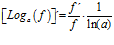
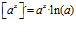
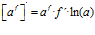
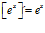
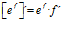
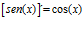
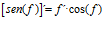
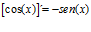
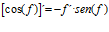
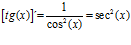
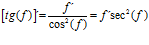
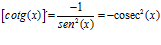
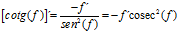
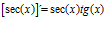
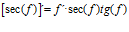
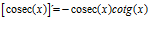
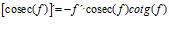
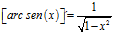
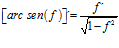
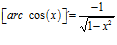

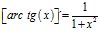
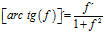
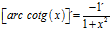
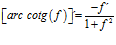
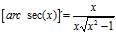
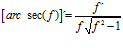
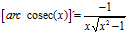
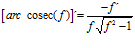
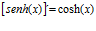
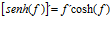
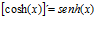
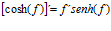
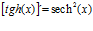
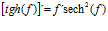
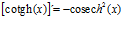
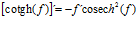
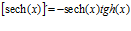

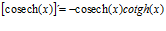
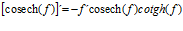
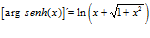
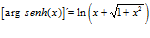
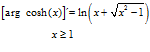
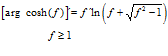
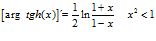

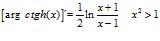
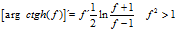
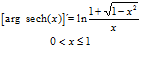
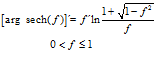
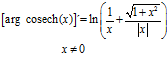
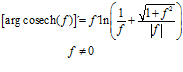

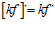
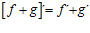
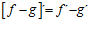
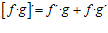
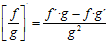

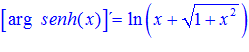
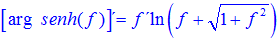
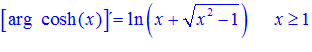
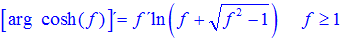
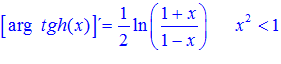
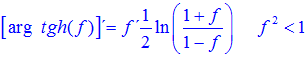
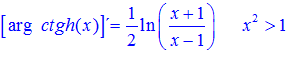
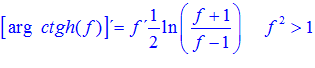
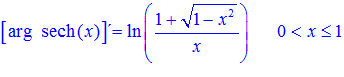
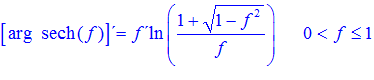
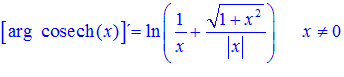
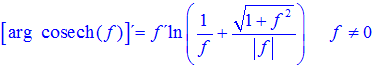
Hay un error en las derivadas de los argumentos de las funciones hiperbólicas:
Ejemplo: FORMULA 25
Cito «LA DERIVADA DEL ARGUMENTO SENO HIPERBÓLICO DE x es igual al logaritmo neperiano de x más la raíz cuadrada de la unidad más x al cuadrado»
Esto hace referencia solo la INVERSA DEL SENO HIPERBÓLICO o dicho de otro modo el ARGUMENTO DEL SENO HIPERBÓLICO.
Corrección: LA DERIVADA DEL ARGUMENTO SENO HIPERBÓLICO DE X es igual a la unida dividida entre la raíz cuadrada de la unidad más x al cuadrado